Mateo

1) Différences finies (2nde)

La suite des carrés des entiers (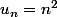) a des écarts de plus en plus grands, donc envisageons la suite des écarts de deux termes consécutifs (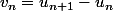), elle augmente moins vite, donc continuons :  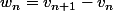et nous obtenons la suite constante égale à 2. Surprenant, non ?

La suite des cubes des entiers, puis des puissances 4 des entiers, etc... Conjecturons qu'au bout d'un nombre fini d'étapes, pour les puissances  on aboutissait à , ce qui peut se démontrer par de longs calculs.

Si on considère que les différences de termes consécutifs sont une approximation de la dérivée, la dérivée  de  est 

2) Sangakus : cercles tangents dans un carré (2nde)

Un formateur nous a posé un excellent problème ouvert :

Construis la figure ci-contre avec GeoGebra.

Remarque : commence par chercher le cas où les deux cercles ont le même rayon.

Rq : si les 2 cercles ne sont pas exactement tangents, agrandis la figure avec GeoGebra.

 3) Pour les deux cercles de même rayon, une première solution consiste à partir des deux cercles tangents, puis à tracer le carré extérieur.
a) http://math.univ-lyon1.fr/irem/IMG/pdf/disques.pdf
c) Étude de l'aire maximale : http://www.apmep.fr/IMG/pdf/25-2.pdf

4) Triangles égaux et semblables (2nde)

je me permets de vous transmettre un article d'Alexandre Carret :
--- Citation ---
Comme je n'hésite pas à interpréter librement les programmes (grâce à mon bouclier de liberté pédagogique), je fais de grands arrêts sur la notion de démonstration géométrique :

 en particulier, j'insiste dans un premier temps sur les arrières-plans mentaux - la vision du monde - construits et discutés par les hommes  (depuis les grecs pour faire simple) et qui les a conduit à entrevoir les notions de cause, de conséquence, de syllogisme, de science,  d'expérience, etc. (par exemple, je leur dis que nous ne discuterons jamais du "beau" en mathématiques.
D'une part parce qu'il s'agit d'une  catégorie mal définie, socialement, culturellement et temporellement  variable et d'autre part qu'il ne s'agit pas d'une catégorie à travers laquelle le mathématicien pense le monde (heureusement, nous ne sommes pas que mathématiciens) : je décroche alors des murs de ma salle "Cygnes se reflétant en éléphants" et "Drawing hands" pour leur expliquer ce qui m'intéresse dans ces œuvres tout en étant persuadé que leur professeur d'arts plastiques leur en parlerait bien autrement (1)).
Par conséquent, j'oriente tout mon discours sur la géométrie autour de l'idée que tout théorème est démontrable sauf les tout premiers que l'on appelle postulats :


Je dois un grand merci à Philippe Colliard de m'avoir ouvert les yeux sur cette liste et dans son livre sur le fait que nous n'avions pas, au collège, à être jusqu’au-boutiste (chercher le minimum de postulats à poser pour démontrer nos théorèmes) et qu'au contraire poser des postulats forts (comme les égalités de triangles) tout en disant qu'un jour peut-être, dans quelques années, on réfléchirait à construire le plus petit noyau de postulats.


Cette découverte m'a libéré : je ne cherchais plus, en mathématicien, à réduire le nombre des postulats mais en prof de collège à trouver le noyau de postulats suffisant pour ne pas avoir à rentrer dans des considérations difficiles (voire contestables : certaines démonstrations d'Euclide ont fait l'objet de nombreux commentaires à travers les siècles).

Les égalités de triangles sont depuis lors omniprésentes dans mon discours (par exemple, pour démontrer dans les deux sens la relation entre symétrie centrale et parallélogramme - alors qu'avant, avec mes petits postulats euclidiens, je passais vite là-dessus car la montagne me semblait bien trop haute à franchir pour mes élèves).

Je précise que, la plupart du temps, ces démonstrations sont exposées à l'oral, parfois écrites dans le cahier et rarement, je leur demande de me les reformuler. Elles servent plutôt à construire le récit que je tente de leur exposer sur la nature et la structure des résultats géométriques avec lesquels il faut se familiariser au collège.

 A eux, je ne demande que des démonstrations plus simples car paradoxalement, ces théorèmes-postulats, bien que premiers dans la théorie, sont difficiles à utiliser dans des démonstrations en autonomie (contrairement, par exemple, au théorème "les diagonales d'un losange sont perpendiculaires" dont l'intuition est forte chez les élèves et l'usage dans les démonstrations relativement aisé - alors même que la démonstration que je leur en propose s'appuie sur des égalités de triangles).

Amicalement,
-- 
Alexandre Carret. (Son site : http://activmaths.free.fr/ )

--- Fin de citation ---

 Merci à Alexandre Carret.

 P.S. Roland Dassonval a publié une démonstration intéressante du théorème de Ptolémée

--- Citation ---
--- Fin de citation ---

5) Rectangles et périmètres (6ème)


Une élève de 6ème a résolu très rapidement l'exercice suivant :

Un rectangle a 20 cm de périmètre et sa longueur a 5cm de plus que sa largeur.

Quelles sont ses dimensions ?


Au bout de 10 secondes une élève a donné la réponse suivante :

"Si le rectangle était un carré, il aurait 5 cm de côté.

Il faut que sa longueur mesure 5cm de plus que sa largeur, donc je divise 5 cm par 2 (soit 2,5 cm)
puis je l'ajoute à la longueur du carré : 5 cm + 2,5 cm = 7,5 cm ;
puis je la soustrais à la largeur du carré : 5 cm - 2,5 cm = 2,5 cm".

Pourquoi a-t-elle divisé 5 cm par 2 ?

Elle a répondu : "Si on ajoute 5 cm à la longueur et si on soustrait 5 cm à la largeur du carré, alors on obtient 10 cm et 0 cm, donc la différence entre les deux est de 10cm (et non de 5 cm)". 

Impressionnant, non ? 

6) Formats (2nde)


En classe prépa, à la 1ère heure de cours de dessin industriel, le prof a commencé par dire :
"Savez-vous que les dimensions d'une feuille de format A4 (une photocopie usuelle) sont 21 cm sur 21 fois racine(2) ?".

 J'ai regardé autour de moi, mais personne n'a souri ;-)

Mais pourquoi cette précision diabolique ? La précision de 21 x 29,7 n'est-elle pas suffisante ?


L'intérêt de ce format précis est que pour agrandir une photocopie du format A4 en A3, il faut un pourcentage d'augmentation de 141% (racine(2)≈1,41), et pour réduire une photocopie du format A4 en A5, il faut un pourcentage de réduction de 71% (1/(racine(2))≈0,71).

 Si les aires sont multipliées (ou divisées) par 2, alors les longueurs sont multipliées (ou divisées) par racine de 2.

 L'intérêt de ce format est de conserver le rapport Longueur/Largeur = racine(2) dans tous les agrandissements qui doublent l'aire du rectangle.

Ci-contre, on a une représentation à l'échelle du format A0 (le plus grand rectangle, d'aire 1 mètre carré), puis du format A1 (la moitié de A0), puis A2 (la moitié de A1), puis A3 (la moitié de A2), puis A4 (la moitié de A3), puis de A5 (la moitié de A4), puis de A6 (la moitié de A5), etc...

On remarque sur ce dessin que les quatrièmes sommets des rectangles coloriés (qui sont de formats A0, A2, A4 et A6) sont tous sur une même diagonale, alors que leurs 3 autres sommets sont sur le côté gauche ou celui du bas. Si on redressait verticalement les rectangles couchés (A1 ; A3 ; A5), on constaterait que c'est encore le cas.

Plus généralement (en utilisant le théorème de Thalès) on peut démontrer que les rectangles dont le quatrième sommet est sur cette diagonale et les trois autres sommets disposés de manière semblable aux précédents sont tous de la même forme  (c'est-à-dire : Longueur/Largeur=constante) mais seuls ceux qui sont dessinés ont une aire qui est le quart de celle du précédent rectangle (A2 est quart de A0 ; A4 est le quart de A2 ; A6 est le quart de A4, etc...).

Comment pourrait-on définir des parallélépipèdes de même forme ? Par la diagonale commune (en rouge) ?

Dans le dessin ci-contre, le grand parallélépipède a un volume 8 fois plus grand que celui du petit (car pour passer du petit au grand, les longueurs ont été multipliées par 2) mais il suffirait de choisir un point précis de la diagonale commune (point que je vous laisse calculer) pour que le volume du petit soit multiplié par 2 pour obtenir le volume du grand.

En résumé, les imprimantes 3D peuvent reproduire des objets de mêmes formes à différentes échelles, (avec des coefficients d'agrandissement ou de réduction  faciles à calculer pour que les volumes soient multipliés ou divisés par 2). (Le dessin a été fait en perspective avec un point de fuite).

7) Une introduction aux vecteurs (2nde)


Mon professeur de 4ème, Jean Galpin, nous a introduit les vecteurs de la manière suivante :

Il y a plus de 100 ans, les chevaux tiraient les péniches le long des berges des rivières, pour remonter le courant, comme sur le dessin ci-contre.





Le segment en pointillés rouges représente une corde, et les flèches représentent les forces exercées par la corde sur la péniche et par les chevaux sur la corde.


Comment faire pour que la péniche ne s'échoue pas ?







Première réponse : en mettant des chevaux des deux côtés de la rivière, comme sur ce deuxième dessin.


L'inconvénient de cette solution est qu'elle empêche d'autres bateaux de dépasser la péniche ou bien de redescendre la rivière.


Deuxième réponse : en tournant le gouvernail pour diriger la péniche vers la gauche (vers babord), on voit que la force appliquée par le centre du gouvernail sur l'eau est la même que sur le dessin nº2 par les chevaux de babord, mais appliquée à l'arrière (la poupe) de la péniche, donc la péniche va tout droit.








Jean-Jacques Dhénin a écrit :

 Oui, je n'avais pas le même professeur de mathématiques, cependant j'avais probablement le même livre, à savoir Lebossé Hémery.

 Mon professeur de mathématiques, ainsi que mon professeur de physique, au collège d'enseignement général, présentaient les vecteurs de cette façon. Nous comprenions, peut-être, parce que nous étions encore un peu familiers de cette méthode pour tracter les péniches.

 Mais lequel de nos élèves, aujourd'hui, a eu vent de ce mode de transport des impondérables ? 

Aucun commentaire:

Enregistrer un commentaire

Inscription à : Articles (Atom)